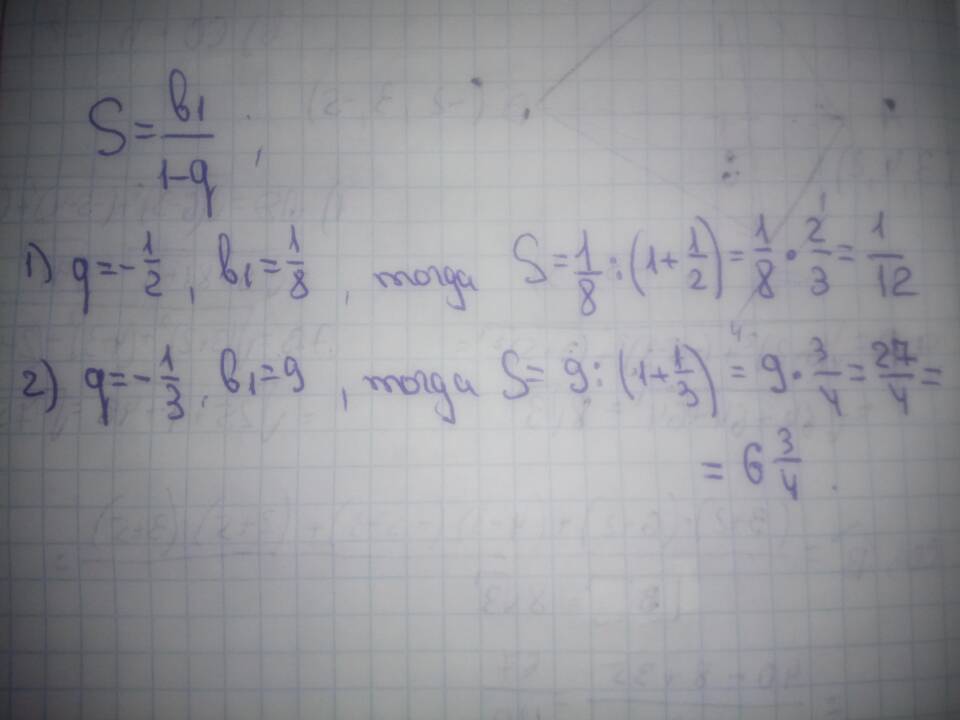Бесконечно убывающая геометрическая прогрессия - это последовательность чисел, где каждый последующий член получается умножением предыдущего на постоянное число q (знаменатель), причем |q| < 1.
Содержание
Определение бесконечно убывающей прогрессии
Формула суммы бесконечно убывающей прогрессии
S = b₁ / (1 - q)
- S - сумма прогрессии
- b₁ - первый член прогрессии
- q - знаменатель прогрессии (|q| < 1)
Условия применимости формулы
| Условие | Пояснение |
| |q| < 1 | Модуль знаменателя должен быть меньше единицы |
| n → ∞ | Количество членов стремится к бесконечности |
Пошаговый алгоритм вычисления
Проверка условий
- Убедитесь, что прогрессия действительно бесконечно убывающая
- Проверьте, что |q| < 1
Определение параметров
- Найдите первый член прогрессии (b₁)
- Вычислите знаменатель прогрессии (q)
Подстановка в формулу
Вставьте полученные значения в формулу S = b₁ / (1 - q)
Примеры вычислений
Пример 1: Простая прогрессия
| Дано | Решение |
| 1 + 1/2 + 1/4 + 1/8 + ... | S = 1 / (1 - 1/2) = 2 |
Пример 2: Прогрессия с десятичной дробью
- 10 + 1 + 0.1 + 0.01 + ...
- b₁ = 10, q = 0.1
- S = 10 / (1 - 0.1) ≈ 11.111...
Графическая интерпретация
Поведение суммы
- С увеличением n сумма приближается к пределу
- Кривая суммы асимптотически приближается к значению S
- Разница между частичной суммой и S становится незначительной
Применение в практических задачах
| Область | Пример использования |
| Физика | Расчет общего пути при бесконечных отражениях |
| Экономика | Определение мультипликативного эффекта |
| Биология | Моделирование ограниченного роста популяции |
Заключение
Формула суммы бесконечно убывающей геометрической прогрессии позволяет найти конечное значение суммы бесконечного числа слагаемых при соблюдении условия |q| < 1. Этот математический инструмент имеет широкое применение в различных научных и практических областях.